For the linear function $g$, the table shows three values of $x$ and their corresponding values of $g(x)$. Function $g$ is defined by $g(x)=ax+b$, where $a$ and $b$ are constants. What is the value of $a-b$? 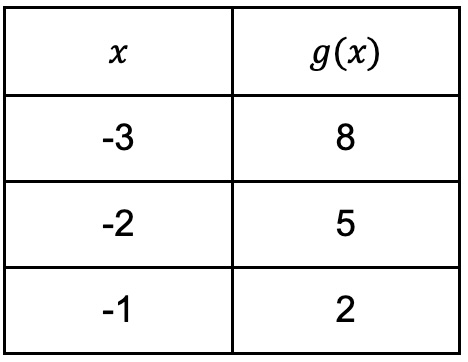

Answer:
B
Explanation
The correct answer is Choice B.
Substitute any two pairs of coordinates into the given function in order to find $a$ and $b$, and therefore, $a-b$.

Choices A, C, and D are incorrect and may result from algebraic mistakes.
✨ Expert's Tip ✨
You can also find $a$, which is the slope of the linear function, using the slope formula: $m=\frac{y_2-y_1}{x_2-x_1}$.