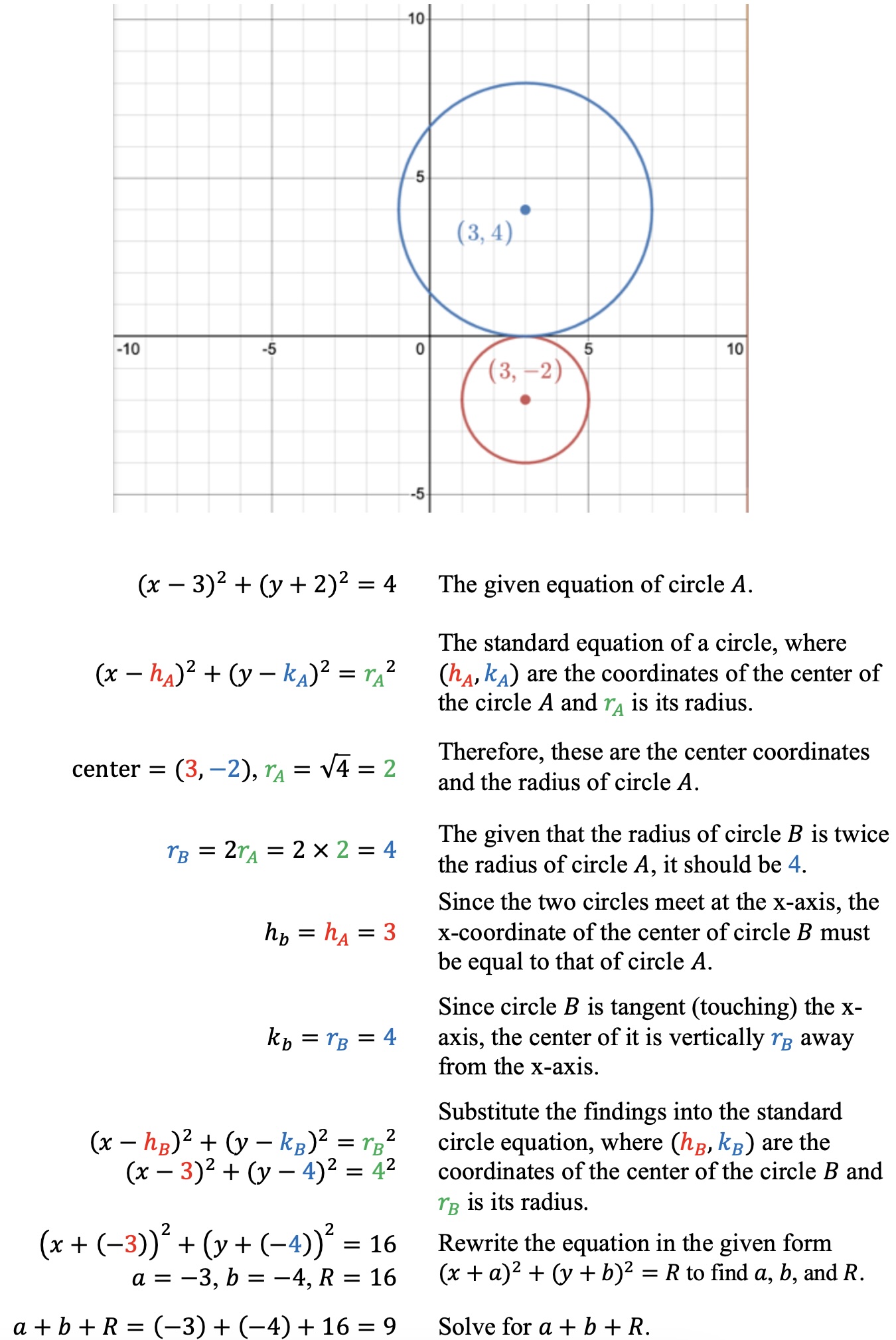
Circle $A$ in the $xy$-plane has the equation $(x-3)^2+(y+2)^2=4$. Circle $B$ meets Circle $A$ at a point on the $x$-axis and has the radius that is twice the radius of Circle A. The equation defining Circle $B$ in the $xy$-plane is $(x+a)^2+(y+b)^2=R$, where $a$, $b$, and $R$ are constants. What is the value of $a+b+R$?
Answer:
Answer:
9
Explanation
The correct answer is $9$.
Use the given equation of circle $A$ and the standard equation of a circle to write the equation of circle $B$ and, therefore, find $a+b+R$.
✨ Expert's Tip ✨
If two circles meet at an axis, they share one same coordinate.